Introduction to K Map
Karnaugh Maps, commonly known as K Maps, are a powerful tool used in the field of digital electronics and computer science for simplifying Boolean algebra expressions. This article aims to provide a detailed yet simplified overview of K Maps. Whether you are just beginning to learn about K Maps or you have a basic understanding but need clarity on how they function, this guide will walk you through the essential aspects.
What is a K Map?
A K Map is a visual representation of truth tables. It allows for the systematic grouping of adjacent cells to simplify complex Boolean expressions, making it easier to design logic circuits. The primary objective of a K Map is to reduce the number of logical operations required in a circuit, thereby streamlining the design process.
The Structure of a K Map
A standard K Map consists of rows and columns, with each cell representing a possible state of the Boolean variables involved. For instance:
- 2-variable K Map: 4 cells (2x2)
- 3-variable K Map: 8 cells (2x4)
- 4-variable K Map: 16 cells (4x4)
Each cell in a K Map corresponds to a minterm of the logical expression, and their arrangement follows Gray Code to ensure that only one variable changes at a time when moving between cells.
Why Use K Maps?
The utility of K Maps can be expressed in the following points:
- Simplification: They help reduce the complexity of logic functions by allowing adjacent minterms to be grouped. For more on simplifying expressions, check out Mastering Order of Operations: Simplifying Complex Expressions.
- Visual Aid: The grid layout of the K Map provides a visual way to understand logic relationships better than traditional algebraic methods.
- Minimization: Results in fewer logic gates needed in hardware implementation, thereby saving space and resources.
Identifying Variables
Before diving into the K Map process, it's essential to identify the variables involved in your logical expression. Variables can be represented by letters such as A, B, C, and D. The number of variables determines the size of the K Map:
- 1 Variable (A): A K Map with 2 cells (0,1)
- 2 Variables (A, B): A K Map with 4 cells (00, 01, 10, 11)
- 3 Variables (A, B, C): A K Map with 8 cells[000, 001, 010, 011, 100, 101, 110, 111]
Filling the K Map
Once you have your K Map set up, it’s time to fill it in:
- Prepare a Truth Table: List all the combinations of the variables.
- Identify Minterms: For each combination, identify where the output is true (1).
- Fill the Map: Place a 1 in the appropriate cells corresponding to the minterms and 0s in the others.
Example of Filling a K Map
Consider a function with three variables A, B, C producing the following output:
| A | B | C | Output | |---|---|---|--------| | 0 | 0 | 0 | 1 | | 0 | 0 | 1 | 0 | | 0 | 1 | 0 | 1 | | 0 | 1 | 1 | 1 | | 1 | 0 | 0 | 0 | | 1 | 0 | 1 | 1 | | 1 | 1 | 0 | 1 | | 1 | 1 | 1 | 0 |
From this truth table, we can fill our K Map.
Grouping Minterms
The next crucial step in K Map simplification is to group the adjacent minterms (1s). Groups must be in powers of 2 (1, 2, 4, 8, etc.). Adjacency can be top, bottom, left, or right, and even wrap around edges:
- One 1: Isolated cell.
- Two 1s: Horizontal or vertical pair.
- Four 1s: Form a rectangle encompassing four adjacent cells.
- Eight 1s: Completion of a larger rectangle.
Rules for Grouping
- Groups should include as many 1s as possible.
- Each 1 must be included in at least one group.
- Groups can overlap.
- Aim for larger groups as they lead to simpler expressions.
Deriving the Simplified Expression
Once the K Map is filled and grouped, the next step is to derive the simplified Boolean expression. Each group corresponds to a product term, which reflects the variables that stay constant for the 1s in that group.
- For each group:
- If a variable remains the same (0 or 1), include it in the product term.
- If a variable changes (both 0 and 1 are present), do not include it in that product term.
Final Expression Example
For groups derived from our example, we can create a simplified expression like this:
- The resulting Boolean expression from the K Map will be a concise version of the original, minimizing redundancy and complexity.
Conclusion
Karnaugh Maps offer an insightful approach to simplifying Boolean algebra expressions, making them crucial for anyone working in digital electronics or related fields. By visualizing the relationships between variables and utilizing grouping strategies, K Maps streamline the minimization of logical operations, leading to effective circuit design. With practice and understanding, anyone can master K Maps and utilize them to their full potential in logic minimization.
To reinforce your learning, I encourage you to review K Map examples and practice constructing and simplifying your K Maps. For additional insights on understanding operations in mathematics, you might find Understanding the Order of Operations in Mathematics helpful. Happy mapping!
from this presentation we will start our k map for the person who already know the what is k map or for the person who dont know what is a kmap
why because we will see a very simple way to understand and also for the one who just know how to solve the kmap,but dont know what actually is going inside a kmap i recommend you to see the lecture till the end
so the kmap is an abbreviation for your karnaugh map as you already know the logic minimization
Heads up!
This summary and transcript were automatically generated using AI with the Free YouTube Transcript Summary Tool by LunaNotes.
Generate a summary for freeRelated Summaries

Understanding Boolean Functions: Sum of Products and Product of Sums
This video tutorial explains how to represent Boolean functions in both Sum of Products (SOP) and Product of Sums (POS) forms. It covers the concepts of minterms and maxterms, providing examples and clarifying the differences between canonical and non-canonical forms.

Understanding Java Short Circuit Operations: A Comprehensive Guide
Explore Java short circuit operations, including examples and benefits for improved performance in programming.

Mastering Verilog: A Comprehensive Guide to Digital Design and Programming
Unlock the secrets of Verilog programming for digital systems. Learn from basics to advanced topics with ease!
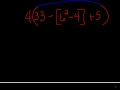
Mastering Order of Operations: Simplifying Complex Expressions
Learn how to simplify complex expressions using the order of operations with clear examples and step-by-step instructions.

How to Simplify Algebraic Expressions: A Step-by-Step Guide
Learn how to simplify algebraic expressions with easy steps and clear examples.
Most Viewed Summaries

Kolonyalismo at Imperyalismo: Ang Kasaysayan ng Pagsakop sa Pilipinas
Tuklasin ang kasaysayan ng kolonyalismo at imperyalismo sa Pilipinas sa pamamagitan ni Ferdinand Magellan.

A Comprehensive Guide to Using Stable Diffusion Forge UI
Explore the Stable Diffusion Forge UI, customizable settings, models, and more to enhance your image generation experience.

Pamamaraan at Patakarang Kolonyal ng mga Espanyol sa Pilipinas
Tuklasin ang mga pamamaraan at patakaran ng mga Espanyol sa Pilipinas, at ang epekto nito sa mga Pilipino.

Mastering Inpainting with Stable Diffusion: Fix Mistakes and Enhance Your Images
Learn to fix mistakes and enhance images with Stable Diffusion's inpainting features effectively.

Pamaraan at Patakarang Kolonyal ng mga Espanyol sa Pilipinas
Tuklasin ang mga pamamaraan at patakarang kolonyal ng mga Espanyol sa Pilipinas at ang mga epekto nito sa mga Pilipino.

