Introduction
Simplifying algebraic expressions is a crucial skill in mathematics, often used in various equations and real-world applications. This guide walks you through essential methods such as distribution and combining like terms. We will discuss several examples, ensuring clarity on how to simplify expressions effectively.
Understanding Algebraic Expressions
An algebraic expression is a combination of numbers, variables, and operations. For instance, the expression 7(s + 9) + 2s involves distributing and simplifying to find a clearer representation.
Key Concepts
- Distribution: The process of multiplying a term by each term inside parentheses.
- Combining Like Terms: Adding or subtracting terms that have the same variable to simplify an expression.
Example 1: Simplifying 7(s + 9) + 2s
Let's break down the expression 7(s + 9) + 2s step by step:
-
Distribute the 7:
- Multiply 7 by s and 9:
- 7 * s = 7s
- 7 * 9 = 63
- So, we rewrite the expression as:
- 7s + 63 + 2s
- Multiply 7 by s and 9:
-
Combine Like Terms:
- Combine 7s and 2s:
- 7s + 2s = 9s
- Thus, the expression simplifies to:
- 9s + 63
- Combine 7s and 2s:
Example 2: Simplifying -4 - (q - 10) + 5
Next, we will simplify the expression -4 - (q - 10) + 5:
-
Distribute the Negative Sign:
- Remember that distributing the negative sign is similar to multiplying by -1:
- -1 * q = -q
- -1 * -10 = +10
- The expression can now be rewritten as:
- -4 - q + 10 + 5
- Remember that distributing the negative sign is similar to multiplying by -1:
-
Combine Like Terms:
- First, combine the constant terms:
- -4 + 10 + 5 = 6 + 5 = 11
- The simplified expression is:
- -q + 11
- First, combine the constant terms:
Example 3: Simplifying -7(i + 2) - 2(2 + i)
Let's move on to -7(i + 2) - 2(2 + i):
-
Distribute the Terms:
- For -7(i + 2):
- -7 * i = -7i
- -7 * 2 = -14
- For -2(2 + i):
- -2 * 2 = -4
- -2 * i = -2i
- Thus, our expression now looks like:
- -7i - 14 - 4 - 2i
- For -7(i + 2):
-
Combine Like Terms:
- Combine -7i and -2i:
- -7i - 2i = -9i
- Combine the constant terms:
- -14 - 4 = -18
- The final simplified expression is:
- -9i - 18
- Combine -7i and -2i:
Conclusion
The art of simplifying algebraic expressions involves understanding the distribution of terms and effectively combining like terms. Whether you’re working with simple expressions or more complex equations, these steps will help you achieve a clear and simplified result. Always remember to keep practice as your priority to master this essential math skill!
let's simplify some of these expressions so this first one is seven times the quantity s plus nine plus two s so we
can distribute the seven because seven is times the entire quantity s plus nine so it's we want to distribute the seven
so it becomes seven times s which is 7s plus 7 times 9 which is 63 and so that's this part right over here
and then we have the plus 2s plus 2s well if i have 7s's if i have 7s's and i'm going to add
another two s's to them i'm going to have nine s's so you add those two parts you get 9s and then you still have your
plus 63. let's do this one over here negative 4 minus the quantity q minus 10 plus five
so what i'm going to do here so we can get rid of this these parentheses is distribute the negative sign this is
essentially multiplying both of these terms times negative one you could view that there's a negative one out here
then this part right over here becomes negative 1 times q or negative times q so it's negative q
negative q and negative 1 times negative 10 is positive 10 plus 10. so that's that part right over there and we still
have this negative 4 out front and this plus 5 afterwards so what can we do over here so we can add all the non-q the
only q term here is this negative q so i'll just rewrite it over here negative q
and then we have all of our constant terms we have negative four plus ten
plus five so negative four plus ten is six plus five is eleven plus eleven negative q plus and the rest
of this adds up to eleven let's do this one all right so we have negative seven times the quantity i plus two so we can
distribute the negative seven so this is going to be equal to negative seven times i which is negative seven i
plus negative 7 times 2 which is negative 14 or we could write plus negative 14 or we could just write minus
we could just write minus 14. so that's this part right over here and then we have negative 2 so this is a
negative 2 times the quantity 2 plus i so that's times 2 and then that's times i so negative 2 times 2 is negative 4 so
it's negative 4. negative 2 times positive i is negative 2i and now we can add the i terms
we have negative 7i and we have negative 2i negative 7i minus 2i is negative 9i
negative 9i and then negative 14 minus 4 those are our constant terms that gives us
negative 18. negative 14 minus 4 is negative 18 and we are done
Heads up!
This summary and transcript were automatically generated using AI with the Free YouTube Transcript Summary Tool by LunaNotes.
Generate a summary for freeRelated Summaries
Mastering Order of Operations: Simplifying Complex Expressions
Learn how to simplify complex expressions using the order of operations with clear examples and step-by-step instructions.
Understanding the Distributive Property and Key Algebra Terms
Learn about the distributive property and important algebra terms like terms, coefficients, and constants.
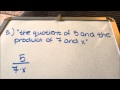
Translating Verbal Expressions into Mathematical Expressions
Master the art of translating verbal expressions into math with clear examples and explanations.
Understanding the Order of Operations in Mathematics
Learn the importance of the Order of Operations and how to solve math problems accurately.
Mastering Square Roots of Rational Numbers: A Comprehensive Guide
Learn how to easily calculate square roots of rational numbers with practical examples and tips.
Most Viewed Summaries
A Comprehensive Guide to Using Stable Diffusion Forge UI
Explore the Stable Diffusion Forge UI, customizable settings, models, and more to enhance your image generation experience.
Pamaraan at Patakarang Kolonyal ng mga Espanyol sa Pilipinas
Tuklasin ang mga pamamaraan at patakarang kolonyal ng mga Espanyol sa Pilipinas at ang mga epekto nito sa mga Pilipino.
Pamamaraan at Patakarang Kolonyal ng mga Espanyol sa Pilipinas
Tuklasin ang mga pamamaraan at patakaran ng mga Espanyol sa Pilipinas, at ang epekto nito sa mga Pilipino.
Kolonyalismo at Imperyalismo: Ang Kasaysayan ng Pagsakop sa Pilipinas
Tuklasin ang kasaysayan ng kolonyalismo at imperyalismo sa Pilipinas sa pamamagitan ni Ferdinand Magellan.
Ultimate Guide to Installing Forge UI and Flowing with Flux Models
Learn how to install Forge UI and explore various Flux models efficiently in this detailed guide.
If you found this summary useful, consider buying us a coffee. It would help us a lot!