Question 1: Square Area as a Function of Perimeter
Given Function
- Area function: A(P) = P2 / 16, where P ≥ 0 (P is the perimeter of the square).
- Graph is considered for 0 ≤ P ≤ 20.
Part A: Calculate A(20) and A−1(12)
- Calculate A(20):
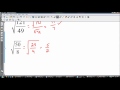
- Substitute P = 20 into A(P): (20)2 / 16 = 400 / 16 = 25.
- Find inverse A−1(12):
- Solve A(P) = 12 → P2 / 16 = 12 → P2 = 192 → P ≈ 13.9.
- Thus, A−1(12) = 13.9.
Part B: Graphing the Inverse Function
- Draw the line y = x as a reference.
- Use points from the original function, e.g., (8,4), and switch coordinates to (4,8) for the inverse.
- Plot these points and sketch the inverse curve.
Part C: Interpretation of Inverse
- A−1(4) = 8 means a square with area 4 has a perimeter of 8.
Question 2: Function with Square Root
Given Function
- f(x) = 7 - 4√(x + 5).
Domain and Range
- Domain: x + 5 ≥ 0 → x ≥ -5.
- Range: Since the square root is non-negative and multiplied by -4, the maximum value of f(x) is 7 (when x = -5).
- Therefore, range is y ≤ 7.
Finding Inverse Value
- Find f−1(2):
- Set f(x) = 2 → 7 - 4√(x + 5) = 2.
- Solve for x using calculator or algebra: x ≈ 3.5.
Question 3: Rational Function Analysis
Given Function
- G(x) = 1 - 3 / (1 - a x).
Part A: Find a given point (2,2)
- Substitute x=2, G(2)=2:
- 2 = 1 - 3 / (1 - 2a).
- Solve for a: a = 2.
- Updated function: G(x) = 1 - 3 / (1 - 2x).
Part B: Domain and Vertical Asymptote
- Denominator ≠ 0 → 1 - 2x ≠ 0 → x ≠ 1/2.
- Vertical asymptote at x = 1/2.
Part C: Intercepts
- X-intercept (G(x) = 0):
- 0 = 1 - 3 / (1 - 2x) → solve for x → x = -1.
- Y-intercept (x=0):
- G(0) = 1 - 3 / 1 = -2.
Part D: Evaluate G(5) and G−1(5)
- G(5):
- G(5) = 1 - 3 / (1 - 2*5) = 1 - 3 / (1 - 10) = 1 - 3 / (-9) = 1 + 1/3 = 4/3 ≈ 1.33.
- Find G−1(5):
- Set G(x) = 5 → 1 - 3 / (1 - 2x) = 5.
- Solve for x → x = 0.25.
Summary
This content demonstrates how to:
- Calculate function values and inverses for quadratic and square root functions.
- Graph inverse functions by reflecting points across y = x.
- Determine domain, range, and vertical asymptotes for rational functions.
- Find intercepts and solve for unknown parameters using given points.
- Use calculators effectively to solve equations and verify results.
These techniques are essential for understanding function behavior and solving real-world mathematical problems involving geometry and algebra.
For further reading on related topics, check out these guides:
question one the area a of a given Square can be represented by function a of P = p² / 16 p is greater than or
equal to zero where p is the perimeter of the square the graph of a function for p greater than equal to0 less than
or equal to 20 is shown below a find the values of a of 20 and inverse of a of 12 a of for
20 we will change every single P into 20 20 squar over 16 =
25 inverse of f of a this a is y and y equal f of x which
means f of x = a so inverse of a of 12 we are looking for a of P equal
12 a of P equals p² over 16 = 12 go to calculator control
divide p² over
16 = 12 control menu enter enter
enter P equals 13.9 by solver P =
13.9 which means the inverse a of 12 equals 13.9 B draw the graph of a inverse
function on the grade first step we need to draw y = x so find 4 4 8 8 12
12 16 16 2020 draw this thought to the line the
intersections for these two graphs will be the points on the inverse function on the original
graph we need to get some more coordinates 8 4 we will switch into
48 F the four fun8 is here then we can sketch the graph like this
normally three points determine a curve in the context of the question explain the meaning of inverse a of four =
8 we do know this is a y and here is x in this function area is y
then perimeter is X which means uh the square whose area is
four has a perimeter of eight question two a function is defined by 7 - 4 < TK x + 5 determine the domain
since this is a square root of function domain is to make
radic x + 5 greater than or equal to zero so X greater than or equal to -5 range
constant number is a seven so y here is a seven a is
A4 y less than or equal to 7 we can put this into graphing calculator to figure out domain and
range 7 minus 4
square root x + 5 enter let's change the window go to four
zoom out we will make inside this square root equals zero so x = 5 go to menu
five enter -5 enter we will get this uh starting
point 57 so X greater than or equal to -5 Y is a less than or equal to 7 find the value
of inverse of f of -2 of 6 + 7 inverse of f of a means f of x =
a we will set up F ofx = -2 6 + 7 f ofx is 7 - 4 < TK x + 5 =
-2 6 + 7 we will type this uh equation into this uh calculator control menu keep
enter x = 3.5 so inverse of f of 2 of 6 + 7 =
3.5 question 3 G of x = 1 - 3 over y - a x h 22 is on the graph of G find the value of a plug back into this function
2 = 1- 3 over 1 - A * 2
simplify 2 = 1 - 3 over 1 - 2 a type the whole equation into this
calculator control menu enter enter enter a equal 2 so we got the function G of x = 1 - 3 over 1 -
2x B write down the domain and a vertical ASM toote line domain since this is a rational
function we will make a denominator not equal to zero minus one both sides -2X is not equal to -1 ided
by -2 both sides X not = to 12 so vertical ASM to line x = 1 / 2 say find the X and V intercept for x
intercept we will set up for G of x = z 1 - 3 over 1 - 2x = Z solve this by solver control
menu enter enter enter x = -1 netive one Z is a x
intercept for y intercept we need to figure out G of zero every single X tur into 0 1 - 3
over 1 - 2 * 0 1 - 3 over 1 is 3 = -2 so 0 -2 is the V
intercept D find the value of for G of5 and a inverse g of5 g
of5 change every single X into -5 1 - 3 over 1 - 2 * 5 go to calculator 1 minus control
divide 3 over 1 - 2 * 5
enter 8 over 11 for inverse of G of5 we do know inverse G of a
means G of x = a so we set how G of x =
5 1 - 3/ 1 - 2x = 5 type the equation into
calculator control menu enter enter enter X = 0.25 which means the inverse G
of-5 = 0.25
To find the x-intercept of G(x), set G(x) = 0 and solve for x. For G(x) = 1 - 3 / (1 - 2x), setting it to zero gives x = -1. For the y-intercept, substitute x = 0 into the function, resulting in G(0) = 1 - 3/1 = -2.
To calculate the area of a square based on its perimeter, use the formula A(P) = P² / 16. For example, if the perimeter P is 20, substitute it into the formula: A(20) = (20)² / 16 = 400 / 16 = 25. This means the area of the square is 25 square units.
The inverse function A⁻¹(A) can be found by solving the equation A(P) = A for P. For instance, to find A⁻¹(12), set P² / 16 = 12, which leads to P² = 192, giving P ≈ 13.9. Thus, A⁻¹(12) = 13.9.
To graph the inverse of a function, first plot the original function's points, then reflect those points across the line y = x. For example, if the original function has a point (8, 4), the inverse will have the point (4, 8). Continue this process for other points to sketch the inverse curve.
The domain of f(x) is determined by the condition x + 5 ≥ 0, which means x must be greater than or equal to -5. The range is y ≤ 7, as the maximum value occurs when x = -5, resulting in f(-5) = 7.
To find the vertical asymptote of the function G(x), set the denominator equal to zero. For G(x) = 1 - 3 / (1 - ax), the vertical asymptote occurs when 1 - ax = 0, leading to x = 1/a. For example, if a = 2, the vertical asymptote is at x = 1/2.
To evaluate G(5), substitute x = 5 into the function: G(5) = 1 - 3 / (1 - 2*5) = 1 - 3 / (1 - 10) = 1 + 1/3 = 4/3, which is approximately 1.33.
Heads up!
This summary and transcript were automatically generated using AI with the Free YouTube Transcript Summary Tool by LunaNotes.
Generate a summary for freeRelated Summaries
Mastering Square Roots of Rational Numbers: A Comprehensive Guide
Learn how to easily calculate square roots of rational numbers with practical examples and tips.

Comprehensive Algebra 2 Guide: Binomials, Exponents, and Inverses
Explore key Algebra 2 concepts including multiplying binomials using FOIL, solving quadratic equations, understanding exponent rules, radicals, and inverse functions. This guide breaks down complex topics with clear examples and actionable insights.

Mastering Function Operations and Composition in Algebra
Explore how to evaluate functions with algebraic expressions, perform arithmetic operations on multiple functions, and understand composite functions with clear examples. Learn the impact on function domains and how to handle complex function compositions effectively.

Understanding the Square Root Symbol: A Comprehensive Guide
Explore the meaning of the square root symbol, its applications, and how to derive values through detailed examples.

Understanding Inverse Trigonometric Functions: A Comprehensive Guide
In this video, Shivani Sharma introduces the concept of inverse trigonometric functions, focusing on Exercise 2.1 from the Class 12 syllabus. The session covers essential concepts, including the domain and range of trigonometric functions, and provides a step-by-step approach to solving related problems.
Most Viewed Summaries

Kolonyalismo at Imperyalismo: Ang Kasaysayan ng Pagsakop sa Pilipinas
Tuklasin ang kasaysayan ng kolonyalismo at imperyalismo sa Pilipinas sa pamamagitan ni Ferdinand Magellan.

A Comprehensive Guide to Using Stable Diffusion Forge UI
Explore the Stable Diffusion Forge UI, customizable settings, models, and more to enhance your image generation experience.

Pamamaraan at Patakarang Kolonyal ng mga Espanyol sa Pilipinas
Tuklasin ang mga pamamaraan at patakaran ng mga Espanyol sa Pilipinas, at ang epekto nito sa mga Pilipino.

Mastering Inpainting with Stable Diffusion: Fix Mistakes and Enhance Your Images
Learn to fix mistakes and enhance images with Stable Diffusion's inpainting features effectively.

Pamaraan at Patakarang Kolonyal ng mga Espanyol sa Pilipinas
Tuklasin ang mga pamamaraan at patakarang kolonyal ng mga Espanyol sa Pilipinas at ang mga epekto nito sa mga Pilipino.

