Introducción
El álgebra nos permite calcular cantidades mediante letras y símbolos, creando un lenguaje matemático que trasciende los números. Este artículo explorará las operaciones con polinomios, brindando una guía completa sobre la terminología matemática fundamental y ejemplos prácticos que harán más accesible el concepto de polinomios.
¿Qué Es un Polinomio?
Un polinomio es una expresión algebraica compuesta por sumas y restas de términos que contienen variables y constantes. Cada término es una combinación de números y variables elevadas a potencias no negativas. Por ejemplo:
- Polinomio: -4x³ - 2x² + 2x - 1
- Polinomio: 3a²bc
- Polinomio: m⁶ - 27
Elementos de un Término Algebraico
Un término algebraico se compone de:
- Coeficiente: El número que multiplica a la variable ( Ej. -8, 4 en -8a, 4mn)
- Parte Literal: Las letras que representan la variable (Ej. x, y, a, b)
- Exponente: El número pequeño que indica la potencia a la que está elevada la variable (Ej. el 2 en x²)
- Signo: Indica si el término es positivo o negativo
Tipos de Polinomios
Los polinomios se clasifican según la cantidad de términos que contienen. Esta clasificación es fundamental para entender cómo se pueden operar y simplificar:
- Monomio: Polinomio con un solo término (Ej. a³)
- Binomio: Polinomio con dos términos (Ej. a³ + 2b)
- Trinomio: Polinomio con tres términos (Ej. a³ + 2b - x)
- Polinomio: Polinomio con cuatro o más términos (Ej. a³ + 2b - x + 6)
Grado de los Polinomios
El grado de un término algebraico se determina sumando los exponentes de las variables presentes en el término. Por ejemplo, en el término 3x²y⁵z⁴:
- Grado = 2 + 5 + 4 = 11
El grado de un polinomio es el mayor grado de los términos que lo componen. Por ejemplo:
- En el polinomio 4x³ - 3x² + 7x⁵, el grado es 5 (por el término 7x⁵)
- En el polinomio 4x²y⁴ - 10 + x⁵, el grado es 6 (por el término x⁵)
Operaciones con Polinomios
Las operaciones fundamentales que se pueden realizar con polinomios incluyen la suma, resta, multiplicación y, en ocasiones, la división. Entender cómo llevar a cabo estas operaciones es esencial para manipular polinomios correctamente.
Suma de Polinomios
Para sumar polinomios, se combinan los términos semejantes:
-
Ejemplo:
(3x² + 5x) + (2x² - 3x) = (3x² + 2x²) + (5x - 3x) = 5x² + 2x
Resta de Polinomios
La resta de polinomios se realiza de manera similar a la suma, restando los coeficientes de los términos semejantes:
-
Ejemplo:
(4x² - 2x + 3) - (x² + 3x - 1) = (4x² - x²) + (-2x - 3x) + (3 + 1) = 3x² - 5x + 4
Multiplicación de Polinomios
La multiplicación de dos polinomios implica el uso de la propiedad distributiva, multiplicando cada término del primer polinomio por cada término del segundo:
-
Ejemplo:
(x + 2)(x + 3) = x^2 + 3x + 2x + 6 = x² + 5x + 6
División de Polinomios
La división de polinomios puede ser más compleja. Se utiliza el método de la división larga o la división sintética:
- Ejemplo: Dividir (6x² + 11x + 3) entre (2x + 1) implica encontrar un cociente y un residuo.
Conclusión
Entender los polinomios y las operaciones que se pueden realizar con ellos es crítico para tener éxito en el álgebra. La terminología y las clasificaciones brindan un camino claro para abordar problemas matemáticos complejos. A medida que te familiarices más con estos conceptos, estas herramientas te serán útiles en estudios avanzados de matemáticas y aplicaciones en diversas disciplinas. No subestimes la importancia de dominar estos fundamentos; son la piedra angular del pensamiento matemático.
etapa 1 operaciones con polinomios la acción 1 terminología algebraica a diferencia de la aritmética que maneja
cantidades concretas o números específicos el álgebra usa además de números otros símbolos generalmente
letras de nuestro alfabeto que representan magnitudes cantidades o valores numéricos no explícitos
el álgebra es la parte de las matemáticas que trata del cálculo de cantidades representando las por medio
de letras nuestras expresiones del lenguaje cotidiano pueden ser representadas por
medio de un lenguaje algebraico como lo veremos en los siguientes ejemplos si quisiéramos representar un número
cualquiera podemos hacerlo por medio de la letra x si quisiéramos representar la mitad de
un número pudiéramos representarlo x entre 2 si quisiéramos representar al que
prácticamente un número aumentado en 1 podríamos hacerlo utilizando la letra a + 1
si quisiéramos representar el producto de dos números podemos representarlo por medio de la letra a b que significa la
multiplicación de un número por otro o bien en el último ejemplo pudiéramos representar el triple de un número
sumado con el doble de otro utilizando la expresión 3x + 2 por otra parte si tuviéramos expresiones
en un lenguaje algebraico podemos representarla utilizando un lenguaje cotidiano como veremos a continuación
por ejemplo si tenemos en la expresión x al cubo esto lo podemos representar en un
lenguaje cotidiano como el cubo de un número en la expresión a +4 en nuestro lenguaje
cotidiano pudiéramos expresarla como la suma de un número con 4 si tenemos la expresión x más elevado al
cuadrado pudiéramos representarlo en nuestro lenguaje cotidiano como el cuadrado de la suma de dos números
en la siguiente expresión tenemos la el término 3a igualados b pudiéramos expresarlo en nuestro lenguaje cotidiano
como el triple de un número sería igual al doble de otro en el último ejemplo tenemos la
expresión a b c que expresada en un lenguaje cotidiano pudiera ser la suma de tres números diferentes
que es un término algebraico pues bien un término algebraico es un número o una letra o el producto de dos o más números
representados por letras por ejemplo el término -8 ave
otro ejemplo 4 m n 6 p o bien menos 2 x al cuadrado estos son
ejemplos de términos algebraicos ahora bien en un término algebraico cualquiera podemos identificar los
siguientes elementos que se mencionan en la imagen por ejemplo empezaremos por el 2
pequeño que viene siendo el exponente las letras que están presentes en el término
son la parte literal el primer número viene siendo el coeficiente
y por último tenemos el signo que puede ser positivo o negativo cualquier combinación de letras y
constantes que contengan las operaciones de suma resta multiplicación división potenciación y radicación ya sea todas o
algunas de ellas recibe el nombre de expresión algebraica por ejemplo la expresión menos 5x cuadrada más 8
otro ejemplo 4 ab - 3 z x 2 o bien la expresión 3 a 2 b c son ejemplos de expresiones
algebraicas que contienen las operaciones mencionadas ya sea de suma resta multiplicación potenciación
etcétera ahora bien cuando en una expresión algebraica aparecen las operaciones de
suma resta multiplicación o potencia la expresión recibe el nombre de polinomio como por ejemplo la expresión menos 4 x
al cubo menos 2 x cuadrada más 2 x menos uno es un ejemplo de un polinomio la siguiente expresión 3 a 2 b c también
es un ejemplo de polinomio así como la expresión m a la sexta menos 27 atendiendo al número de términos que
componen un polinomio este se clasifica de la siguiente manera mono mío es a que el polinomio que tiene
un solo término por ejemplo a kubica binomio es a que el polinomio que tiene dos términos por ejemplo a kubica + 2 b
trinomio es a que el polinomio que tiene tres términos por ejemplo a kubica más 2 b - x
polinomio es aquel que tiene cuatro o más términos por ejemplo a kubica más 2b - x + 6
cuando se tienen cuatro o más términos todos se clasificarán como polinomio de 456 o cualquier número de términos que
contengan el grado de un término algebraico será la suma de los exponentes que aparecen
en la parte literal de dicho término algebraico por ejemplo en el término 3x cuadrada y a la quinta
c 4 para determinar el grado de este término debemos sumar los exponentes que son 25
y 4 sumados nos dan el grado 11 ahora bien el grado de un polinomio será
el mayor de los grados de los términos que lo componen por ejemplo en el polinomio 4 x al cubo menos 3 x
cuadrada más 7 x a la quinta el grado de este polinomio será 5 ya que es el mayor de los grados de los términos que lo
componen en el siguiente ejemplo 4x cuadrada llega a la 46 x a la quinta menos 10 el
grado de este polinomio será 6 ya que es el mayor de los grados de los términos que lo componen
Keep this summary
Save it to LunaNotes and it becomes a real note in your library — editable, searchable, and ready to turn into flashcards or a diagram. Free to start.
Save to LunaNotesOr summarise for another video.
This summary and transcript were automatically generated using AI with the Free YouTube Transcript Summary Tool by LunaNotes.
Related summaries
Operaciones con Polinomios: Introducción al Álgebra
Descubre la terminología y conceptos clave en operaciones con polinomios en álgebra.
Understanding the Distributive Property and Key Algebra Terms
Learn about the distributive property and important algebra terms like terms, coefficients, and constants.
Comprehensive Algebra 2 Guide: Binomials, Exponents, and Inverses
Explore key Algebra 2 concepts including multiplying binomials using FOIL, solving quadratic equations, understanding exponent rules, radicals, and inverse functions. This guide breaks down complex topics with clear examples and actionable insights.
Understanding Quadratic Polynomials: Key Concepts and Formulas
This comprehensive summary covers the essential concepts of quadratic polynomials, including their definitions, types, and key formulas. It also addresses how to find the roots of quadratic equations and the relationships between the coefficients and roots.
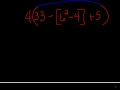
Mastering Order of Operations: Simplifying Complex Expressions
Learn how to simplify complex expressions using the order of operations with clear examples and step-by-step instructions.
Most viewed summaries
A Comprehensive Guide to Using Stable Diffusion Forge UI
Explore the Stable Diffusion Forge UI, customizable settings, models, and more to enhance your image generation experience.
Kolonyalismo at Imperyalismo: Ang Kasaysayan ng Pagsakop sa Pilipinas
Tuklasin ang kasaysayan ng kolonyalismo at imperyalismo sa Pilipinas sa pamamagitan ni Ferdinand Magellan.
Mastering Inpainting with Stable Diffusion: Fix Mistakes and Enhance Your Images
Learn to fix mistakes and enhance images with Stable Diffusion's inpainting features effectively.
Pamamaraan at Patakarang Kolonyal ng mga Espanyol sa Pilipinas
Tuklasin ang mga pamamaraan at patakaran ng mga Espanyol sa Pilipinas, at ang epekto nito sa mga Pilipino.
How to Install and Configure Forge: A New Stable Diffusion Web UI
Learn to install and configure the new Forge web UI for Stable Diffusion, with tips on models and settings.
Found this summary useful?
Take it with you. One click puts it in your own LunaNotes library.
Save to LunaNotes